Recently, Communications Physics, a prominent journal under Nature, published the latest research work from Professor Shiyuan Liu's group on the large-scale electromagnetic field computation method. The paper, titled "Modified Born series with virtual absorbing boundary enabling large-scale electromagnetic simulation", lists doctoral candidate Pinxuan He as the first author, with Professor Shiyuan Liu and Dr. Jiamin Liu as corresponding authors. Professors Honggang Gu and Hao Jiang are co-authors, and State Key Laboratory of Intelligent Manufacturing Equipment and Technology at our university is acknowledged as the hosting institution for this work.

The precise large-scale simulation of the scattering interaction between the light and the complex nanostructures plays a critical role in applied optics. Various rigorous methods, such as Finite-Difference Time-Domain (FDTD), Finite-Difference Frequency-Domain (FDFD), Modified Born Series (MBS), and Finite Element Method (FEM), can perform the electromagnetic field numerical calculations by solving Maxwell's equations. However, when applied to large-scale simulations—spanning thousands of wavelengths, such as metasurface design, biological imaging, and extreme ultraviolet (EUV) lithography—the memory requirements of these methods become a significant bottleneck. Thus, reducing memory consumption is critical to achieving precise large-scale electromagnetic field simulations.
To tackle the challenge, Professor Shiyuan Liu's group proposed a virtual boundary condition. By utilizing pseudo propagation in the Modified Born Series and updating the boundary region’s electric field through angular spectrum methods during iterative electromagnetic field calculations, the virtual boundary condition eliminates the need to store data from absorbing boundary regions. This innovation dramatically reduces memory usage at absorbing boundaries, significantly expanding the scale of simulations feasible under the same hardware.

Figure 1: Pseudo propagation and virtual absorbing boundary in the Modified Born Series
Within this framework, computational errors in the boundary region remain acceptable. Consequently, the thickness of the absorbing boundary can be minimized. Since the boundary fields are recalculated during each iteration, storing these data is unnecessary, further decreasing memory consumption. Compared to traditional absorbing boundaries, VBC's memory footprint is negligible. When integrated with the Fourier-transform-based Modified Born Series, memory usage could approach theoretical limits.

Figure 2: Implementation of the virtual absorbing boundary
The implementation of the angular spectrum method can be integrated with the convolution computation of the modified Born series. By decoupling along the x- and y-axes, these operations can be performed in depth independently, as illustrated in Figure 2. This approach avoids bulky memory usage spikes, significantly improving computational granularity and efficiency.
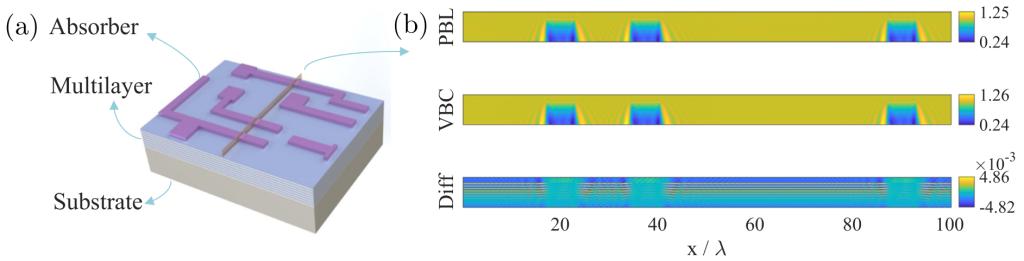
Figure 3: Application and validation of VBC in EUV mask diffraction calculations
The paper provides three examples—plane wave propagation, EUV lithographic mask diffraction, and biological cell scattering—to demonstrate the proposed method's performance. Plane wave propagation serves as a straightforward test case, validated through field amplitude variations. Despite low memory usage, the VBC method outperforms other absorbing boundaries. It also demonstrates stability and accuracy when applied to EUV mask diffraction and biological cell scattering.

Figure 4: Application and validation of VBC in optical diffraction tomography
The proposed virtual boundary condition approach supports implementation via single instruction/multiple data (SIMD) techniques and is extendable to GPU platforms. It holds immense potential for applications such as full-chip EUV computational lithography, computational imaging, metasurface design, and biomedical microscopy.
This research was supported by the National Natural Science Foundation of China (52130504 and 52305577), Key Research and Development Plan of Hubei Province (2021BAA013 and 2022BAA013), Major Program (JD) of Hubei Province (2023BAA008-2), Innovation Project of Optics Valley Laboratory (OVL2023PY003), and Postdoctoral Fellowship Program (Grade B) of China Postdoctoral Science Foundation (GZB20230244).
Paper’s link:https://www.nature.com/articles/s42005-024-01882-5